今回のテーマは平成29年度問21です。

「ＨとＩの座標値を求める計算」において、直線ＨＩ上の仮点Ｍを作る際の考え方についてみていきましょう。
これを理解できると計算に強くなれるので、しっかり覚えておくことをお勧めします。

そもそも何をしようとしているのか

ひとまず状況を整理しておきましょう。
以下の図をご確認ください。

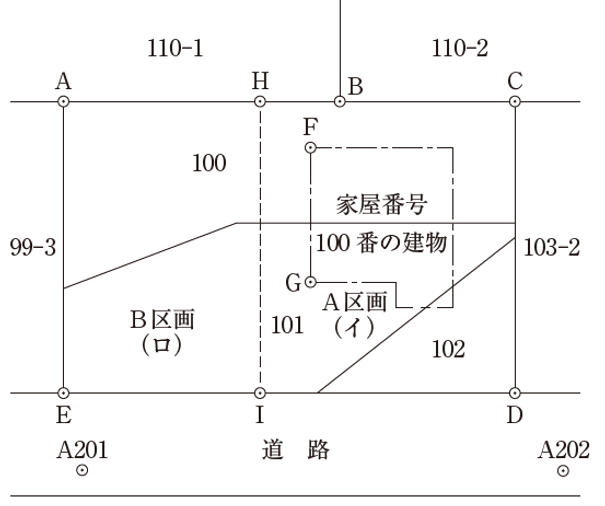
問題の設定は

① 建物の西側側面であるＦとＧを結ぶ直線に平行で、西側に１ｍ移動させたところを分筆線とする
② ①の線と、ＡＢ、ＥＤの交点がそれぞれＨ、Ｉとなる

です。
そこで、ＨとＩの座標値を求めろ、ということですね。
この時点で、どちらも交点計算だな、ということは分かります。

さて、問題文では、以下の青丸の座標については明らかになっています。

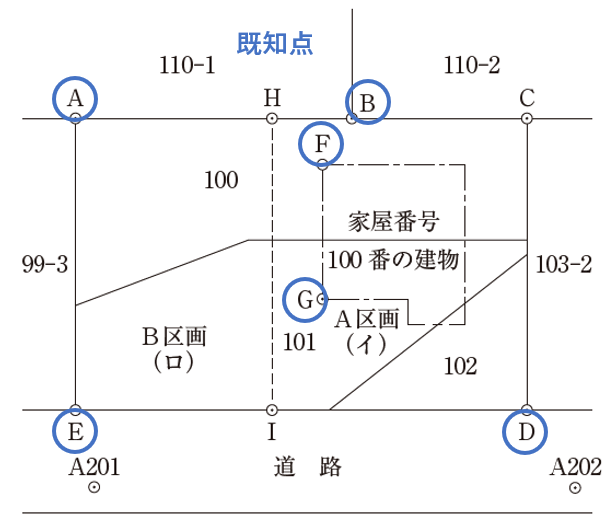
交点計算をする場合、「２本の直線の方向角」と「その２本の直線上の点の座標値」が分かれば、計算することができます。

Ｈを求めるときは、ＡＢとＨＩの交点計算
Ｉを求めるときは、ＥＤとＨＩの交点計算

をすればよいということですね。

ＡＢが既知点ですから、ＡＢの方向角は分かります。
ＥＤが既知点ですから、ＥＤの方向角も分かります。
ＦＧが既知点ですから、ＦＧの方向角も分かります。
そして、ＨＩの方向角は、ＦＧの方向角と同じです（平行なので）。

ＡＢが既知点なので、ＡＢ上の点の座標値はＯＫ。
ＥＤが既知点なので、ＥＤ上の点の座標値はＯＫ。

これによって、あと交点計算に足りないのは「ＨＩ上の点の座標値」である、ということが分かります。
つまり、交点計算をする前提として、まず直線ＨＩ上の点を求めようとしているわけですね。

どうやってＨＩ上の点を求めるのか

さて、ではどうやってＨＩ上の点を求めるのか。
そのヒントとなるのが、「ＨＩは、ＦＧを西側に１ｍ平行移動させた線である」ということです。

ということは、「ＦＧ上にある点」を同様に「西側に１ｍ平行移動」させてあげれば、ＨＩ上の点になります。
ＦＧ上にある点といえば（当たり前ですが）ＦとＧです。
どちらでもいいですが、Ｆを使いましょう。
Ｆを、「西側に１ｍ平行移動」させるのです。

そして、平行移動させた点を「Ｍ」としましょう。
こんなイメージです。

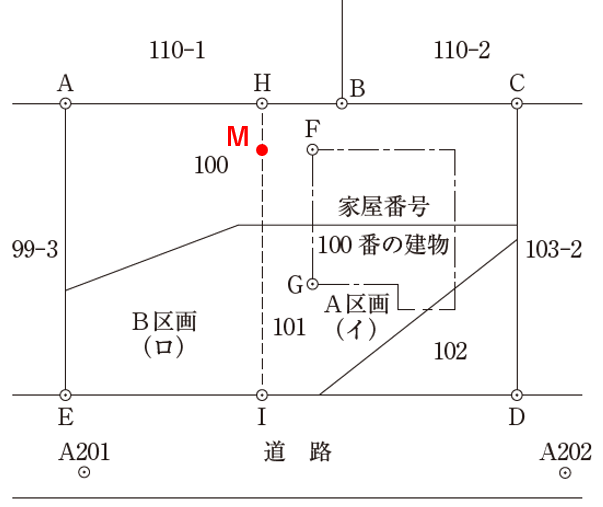
さて、ではＦを移動させてＭの座標値を求めたいと思います。
どういう計算をすればよいでしょうか？この場合は

「ＦからＧの方向角に90°を足した」方向角に１ｍ移動させることになります。

ここが多くの方がつまづかれるところでしょう。
なぜ90°なのか？ということですね。
ここで大事な知識は

平行な２直線間の距離は、その２直線間に引いた垂線の長さになる

ということです。

今ここに２本の適当な線を引きました。
右側の赤い点から、もう１本の直線への距離は一体どこで測るでしょうか？

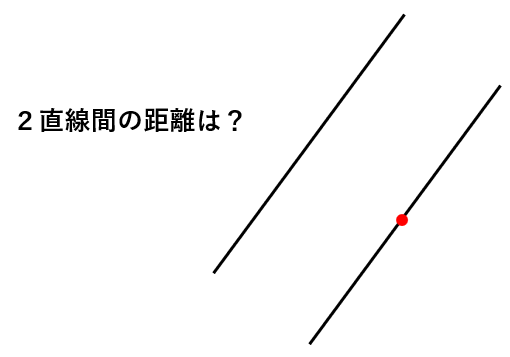
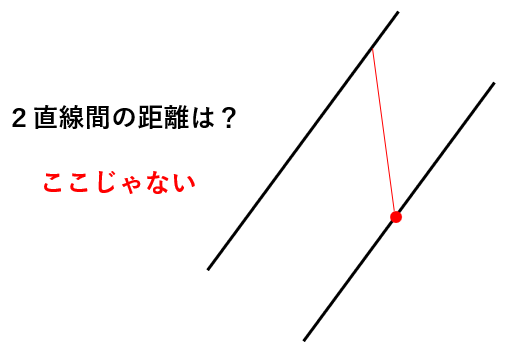
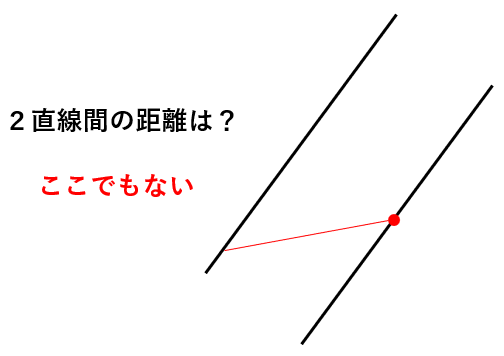
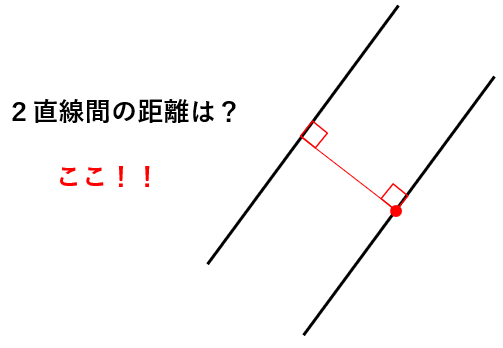
お分かりですか？
平行な直線の間の距離というのは、どちらにも直角に交わる垂線の長さなのです。

本問において、ＦＭの距離が「１ｍ」ということは、ここの距離が１ｍということです。

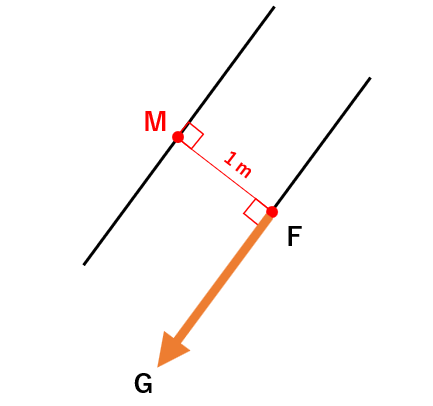
勘のいい方はそろそろお気付きですかね。
この場合、ＦからＭへの方向角は、ＦからＧの方向角に90°を加えた値になるのです。
以下の図をご覧ください。

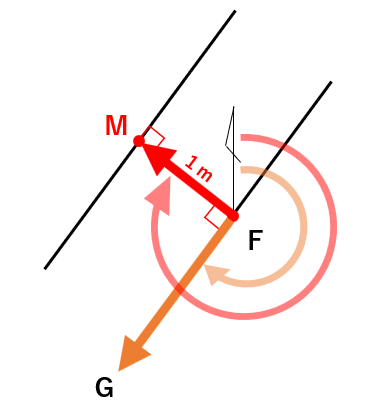
（ＦからＧの方向角がオレンジ、ＦからＭの方向角が赤です）

そのため、まずＦからＧの方向角を求め、それに90°を加えた方向にＦを１ｍ移動させれば、Ｍになる、ということです。
あとは、求めたＭを使って交点計算をしてあげればよいだけです。

「平行移動した線上の点に移動させるときは、方向角に90°の差が生じる」という知識をしっかり覚えておいてください。

ＧからＦの方向角を使う場合は？

「ＧからＦの方向角を使っても90°を足せばいいですか？」

という質問もよく頂きます。
この場合は90°を足してはいけません。
逆に、90°を引きます。

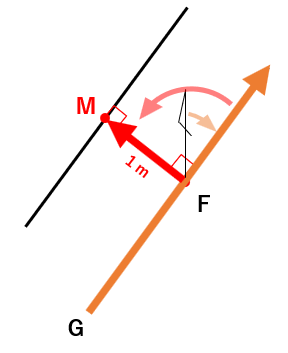
ＧからＦの方向角を使った場合、ご覧の通り、矢印は北向きになりますね。
この矢印の向きを「西側」に向けたいわけですから、回転させる方向は「左回り（反時計回り）」になります。

回転させるときは

• 右回り（時計回り）ならプラス
• 左回り（反時計回り）ならマイナス

にします。
つまり、ＧからＦの方向角を求めて、そこから90°を引いた方向角を使うことになります。
（時計回りの方が分かりやすければ、「270°を足す」でもよいです）

• どこからどこへの方向角を使うか
• その向きをどちらへ向けたいか

によって、プラスにするかマイナスにするかを決めるわけです。

最初はややこしく感じるかもしれませんが、何度かやればすぐに感覚が掴めるはずです。
頑張って計算してみてください。