これもたびたび頂く質問です。

平成23年度問21のＣ点の座標値について、まずＢを求めて、そこからＢＩとＥＭの交点計算でＣを計算したのですが、解答とズレてしまいました。なぜでしょうか。

理由は大きく２つあります。
今回はそれについて説明をしていきます。

理由１　三角関数真数表の存在

平成29年度以前の問題には、「三角関数真数表」があります。
これは、計算において三角関数を使用するときは、この値を使って計算せよ、というものです。

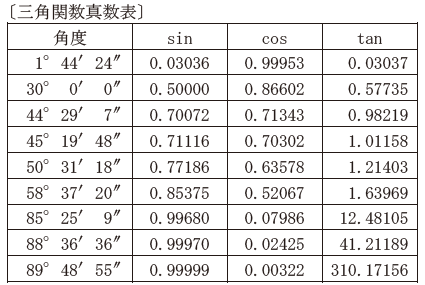
一番左の「角度」をご確認ください。
ものすごく具体的な角度が表示されていますよね。

要は、ここに記載されている角度が、「この問題において使用する可能性のある角度」です。
出題者はこの角度の値を使って解くことを誘導している、ということです。
（昔はこれが計算のヒントになっていたのですね）

つまりですね、ここにない角度を使って計算することは、そもそも出題者の想定の範囲外です。

そのため、この角度を使わないアプローチをすると、出題者の想定した答えとズレることがあるのです。

理由２　ＢＩが直線という記載はない

ＢＩとＥＭの交点計算でＣを計算しました、という方が多いのですが、そもそも「ＢＩが直線」という文言は問題文中にありません。

直線のようには見えますが、「見えるだけ」です。
もともと素図は正確なものではありませんから、「直線に見えること」は根拠になりません。

つまり、計算の前提として、問題文にない設定を使っているのです。
それではダメですよね。
ズレが生じるのは、ある意味で当然といえます。

覚えておくべきこと２つ

ということで、以上から得られる学びは２つ。

・平成29年度以前の問題は、真数表に表示されている値を使うアプローチのみが、出題者が想定している解き方である

今はそういう出題になっていないので安心してください。
平成30年度以降、真数表は撤廃されましたので、複数のアプローチも可能となりました。
（ただ、その分、最初からアプローチ方法が限られていたり、そもそもシンプルな計算が多くなりました）

・問題文にない設定を使ってはいけない

これは本当に大事なことです。
必ず問題文から明らかな情報のみを使うようにしてください。
「複数のアプローチが可能」というのは、あくまで問題文の設定に乗った上で、ということですからね。
ご注意ください。